Our goal is to determine to moment of inertia (MOI) of a physical pendulum using only a video of its motion. We apply image processing techniques to extract necessary information needed to solve for the MOI. We used a flat metal ruler (mass=.0478kg, height=.635m, width=.03m) as the physical pendulum. Below is a sample video of its motion.

The MOI of a physical pendulum is given by:
I=mg(h/2)(T/2π)^2.
(source: http://cnx.org/content/m15585/latest/)
To solve for I, we have to determine the period of oscillation from the video. First, we convert the video into frames of images. In processing the images, we first apply the color image segmentation such that we pick out the moving physical pendulum away from the background. This technique has already been discussed from the previous activity. Below are the results.
Notice that the quality of the images are poor and distorted. We enhance the quality of the images using another technique previously discussed: morphological operations. We first binarized the images then apply dilation and erosion to enhance the shape of the physical pendulum.

Now that the images are enhanced, we determine the period T of the oscillation. Since the images are binarized, we could keep track of the motion of the pendulum by noting the x and y coordinates of the white pixels corresponding to the pendulum. We use the mean x and the mean y coordinate to approximate the motion of the center of mass. Below is the plot of the X axis coordinate as a function of time.
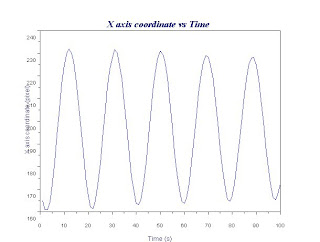
As the oscillation reaches a maximum, there would be a change in the directions of the coordinates of the center of mass. This periodic change in direction is the sinusoidal function we see in the plot above. Noting this and counting the number of frames between consecutive changes, we determine the number of frames corresponding to half the period. Since the frame rate of the video is 14.5 fps, the time interval per frame is 1/14.5=.069s. Thus the half period of the oscillation is just the number of frames times .069s.
From the processed images, the number of frames corresponding to half a period are: 10, 10, 9, 10, 9, 10, 9, 10, 10, 9. The mean value is: 9.6 frames corresponding to 0.6624s half period. Thus, the period of oscillation is 1.3248s. Using the equation above, we determine the MOI to be 6.612E-3.
To check, we determine to moment of inertia using another equation given as:
I=(m/2)(h)^2 + (m/12)(h)^2
(source: http://en.wikipedia.org/wiki/List_of_moments_of_inertia)
Noting the value of the mass=.0478kg, height=.635m, and width=.03m, the theoretical MOI is 6.428E-3. Comparing with the experimental MOI above, this corresponds to 2.86% error. The method is successful in determining the MOI of a physical pendulum using only a video of its motion.
I've successfully accomplished the activity. I want to give myself a 10.
Acknowledgment to my collaborators on the physical pendulum video gathering: Cole and Jeric.