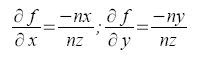..on color image processing

Below are images taken at different white balancing.







Daylight setting under flourescent light











Cloudy setting under flourescent light















Flourescent setting under daylight







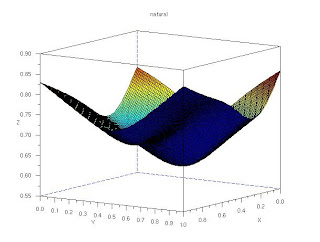
We notice that the images are wrongly balanced. The background which is supposed to be white appears otherwise. The white background for the daylight setting under flourescent light appears greenish. For the second image, the background appears grayish while for the last image, the background appears bluish. In order to correct these, we apply two popular algorithms for achieving automatic white balance: the reference white algorithm and the gray world algorithm.

Reference White Algorithm (RWA)
This method utilizes a known white image and used its RGB values as the divider. For our images, we used the background as the reference white. Below are the results of the enhancement. Notice that we have improved the color of the background as well as the colorful patches.





RWA (Daylight setting under flourescent light)














RWA (Cloudy setting under flourescent light)











RWA
(Flourescent setting under daylight)








Gray World Algorithm (GWA)
This method assumes that the world is essentially gray. Thus, we just take the average of the red, green, and blue value of the captured image and use them as the divider. Below are the resulting enhanced images. Again, the colors of the resulting images are greatly enhanced.







GWA (Daylight setting under flourescent light)













GWA (Cloudy setting under flourescent light)










GWA
(Flourescent setting under daylight)









Finally, we take an image of an ensemble of leaves having the same hue (green). This image is taken in flourescent setting under daylight. Notice that the white background appears bluish. Also, the color of the dark leaves appears black.






Flourescent setting under daylight







We improve this image using the reference white algorithm and gray world algorithm. Below are the resulting images. Both methods were able to enhance the image. The background now appears white and the color of the leaves are enhanced. Between the two methods, the resulting image from the gray world algorithm is better. The background appears really white and the color of the leaves are really distinct and clear.





RWA














GWA







I was able to successfully perform the activity. I want to give myself a 10.

Acknowledgment to Jeric for the rubik's cube and Rica for uploading the images.

..on stereometry

We try to reconstruct the image of a 3D object using images taken at different positions. Using a technique called stereometry, we will derive the depth z of the 3D object using 2D images (x,y). Consider the diagram below.





















Given that the 2 images have the same y coordinates, we could solve for z using:






where b is just the traverse distance between the 2 images and f is just the focal length of the camera. We could solve for f using the calibration technique discussed on the previous activity.

Below are the two different images of a rubik's cube taken with b=5cm.











































Using 25 different points (x,y), we calculated for the corresponding depth (z). Below are the 3D reconstruction using splin2d of scilab for not a knot, bilinear interpolation, natural, and monotone.
















Enlarging further, we see that the reconstructed 3D object depicts a cube. Though the resulting rendition is not a perfect cube, we were able to show the general shape of the 3D object.

















I want to give myself a 10.

..on photometric stereo

We use photometric stereo to extract the 3D shape of an object using only the information from the shadow. We estimate the shape of the object using the shading obtained from different images of different light source location.

Consider a point source of light at infinity.











The intensity I of the image is related to the vector position of the camera given by:








where N is the number of images used. We now solve for g using:




to get the normal vector n, we simply normalize it:





to derive the shape from the normals, we note that the surface elevation f(x,y) is related to the normals by:






Finally, we solve for the surface elevation using:







We apply this technique using four images of a sphere. The resulting 3D rendition is:















Indeed, the resulting shape is a sphere.

I've successfully accomplished the activity. I want to give myself a 10.

..on correcting geometric distortions

Below is an image of a "grid" capiz window. Notice that the image has a barrel distortion effect. The square grids located at the edges are much smaller than those found at the center. The center appears to be bloated while the sides are pinched. These are due to the "imperfect" lens of the camera that captured the image.

















Our goal is to correct this distortion. We use the center square grid as our reference since it is less distorted. We then determine the transformation matrix that caused the barrel effect. Let f(x,y) be the coordinates of the ideal image while g(x',y') are the coordinates of the the distorted image. To determine the transformation matrix C, we map the coordinates of the ideal image in the distorted image.










We then compute for the transformation matrix C using:






Now that we have determined the transformation matrix, we just simply copy the graylevel v(x',y') of the pixel located in g(x',y') into f(x,y). But since the calculated g(x',y') coordinates are real (pixel coordinates should be integral), we use bilinear interpolation. The graylevel of an arbitrary point is determined by the graylevel of the 4 nearest pixels encompassing that point.













We can no solve for the graylevel using:




For the remaining blank pixels in the ideal image, again we use interpolation of the four nearest corners to determine its graylevel. Below is a comparison of the original distorted image and the enhanced(ideal) image. Notice that at the lower left level, the size of the square grid for the enhanced image increased. The grid lines also become more parallel. The resulting image has lessen the effect of the distortion. The image is no more bloated.






Original distorted image











Enhanced ideal image









I think I've performed the activity successfully. The distorted image was enhanced. I want to give myself a 10.